HF Riego Excel: Factor de Salidas Múltiples
1. Ecuaciones
La reducción del caudal por cada salida, hace que la pérdida de carga por fricción se deba calcular segmento a segmento, desde la última salida aguas abajo hasta la primera aguas arriba (Ángeles et al., 2007). Este procedimiento se puede simplificar si solamente se desea calcular la pérdida por fricción de principio a fin del tubo, sin importar la distribución de la presión intermedia.
Esto indica que la pérdida de carga por fricción en una tubería con salidas múltiples (hfs) se puede determinar calculando la pérdida de carga en una tubería simple o ciega del mismo diámetro, longitud y con el mismo gasto de entrada, multiplicando sólo por un factor de salidas múltiples (F).
$${ hf }_{ s }=hf*F$$
El método mas conocida para determinar el factor de salidas múltiples es el de christiansen (1942), este método se utiliza cuando la distancia a la primera salida es igual al espaciamiento entre salidas consecutivas
$${ F }_{ 1 }\quad =\frac { 1 }{ m+1 } +\frac { 1 }{ 2N } +\frac { \sqrt { m-1 } }{ 6{ N }^{ 2 } } \quad $$
$${ F }_{ 1 }\quad =\frac { 1 }{ m+1 } +\frac { 1 }{ 2N } +\frac { \sqrt { m-1 } }{ 6{ N }^{ 2 } } \quad $$
donde: Dónde; F1
es el factor de salidas múltiples de Christiansen; N es el número de salidas; m
es el exponente de la velocidad en la fórmula usada para calcular la pérdida de
presión causada por la fricción.
La ecuación 2, supone que:
Cuando la distancia del inicio de la tuberia a la primera salida es igual a la mitad (S0 = S/2) del espaciamiento de los demás salidas, el F2 se calcula usando el método de Jensen & Fratini (1957):
- La distancia entre salidas es constante,
- El caudal de cada salida es constante,
- La distancia del inicio de la tubería a la primera salida (S0) es igual al espaciamiento del resto de salidas (S),
- Después de la última salida el caudal es cero y el material y el diámetro de la tubería se mantienen constantes.
$${ F }_{ 2 }\quad =\frac { 2N }{ 2N-1 } \left[ \frac { 1 }{ m+1 } +\frac { \sqrt { m-1 } }{ 6{ N }^{ 2 } } \right] \quad $$
Debido a que en campo la primera salida no siempre se encuentra a una distancia constante, Scaloppi (1988), derivó un F tomando como base la ecuación propuesta por Christiansen, donde el espaciamiento desde el inicio de la tubería a la primera salida puede ser cualquier distancia, la expresión de dicho factor es:
$${ F }_{ 3 }=\frac { N{ F }_{ 1 }+rs-1 }{ N+rs-1 } \quad $$
2. Como usar las formulas
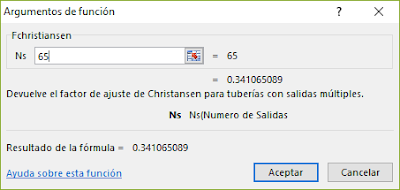
HF Riego tiene la opción de calcula el factor de salidas múltiples mediante los tres métodos, solo debe dar clic en el icono de funciones y seleccionar el que desee (ver figura):
para determinar el factor de salidas con los métodos de christiansen y Jensen & Fratini únicamente se necesita ingresar el numero de salida (N), el valor de m lo toma de la método para estimar la perdida de carga por fricción [Manning, Scobey, Hazen-Williams] que se seleccionó en ajustes:
para el método de Scaloppi es necesario ingresar el Numero de salida (N), distancia a la primera salida (S0) en m y distancia entre salidas consecutivas (S).
¿Falto algo?, déjanos tus comentarios



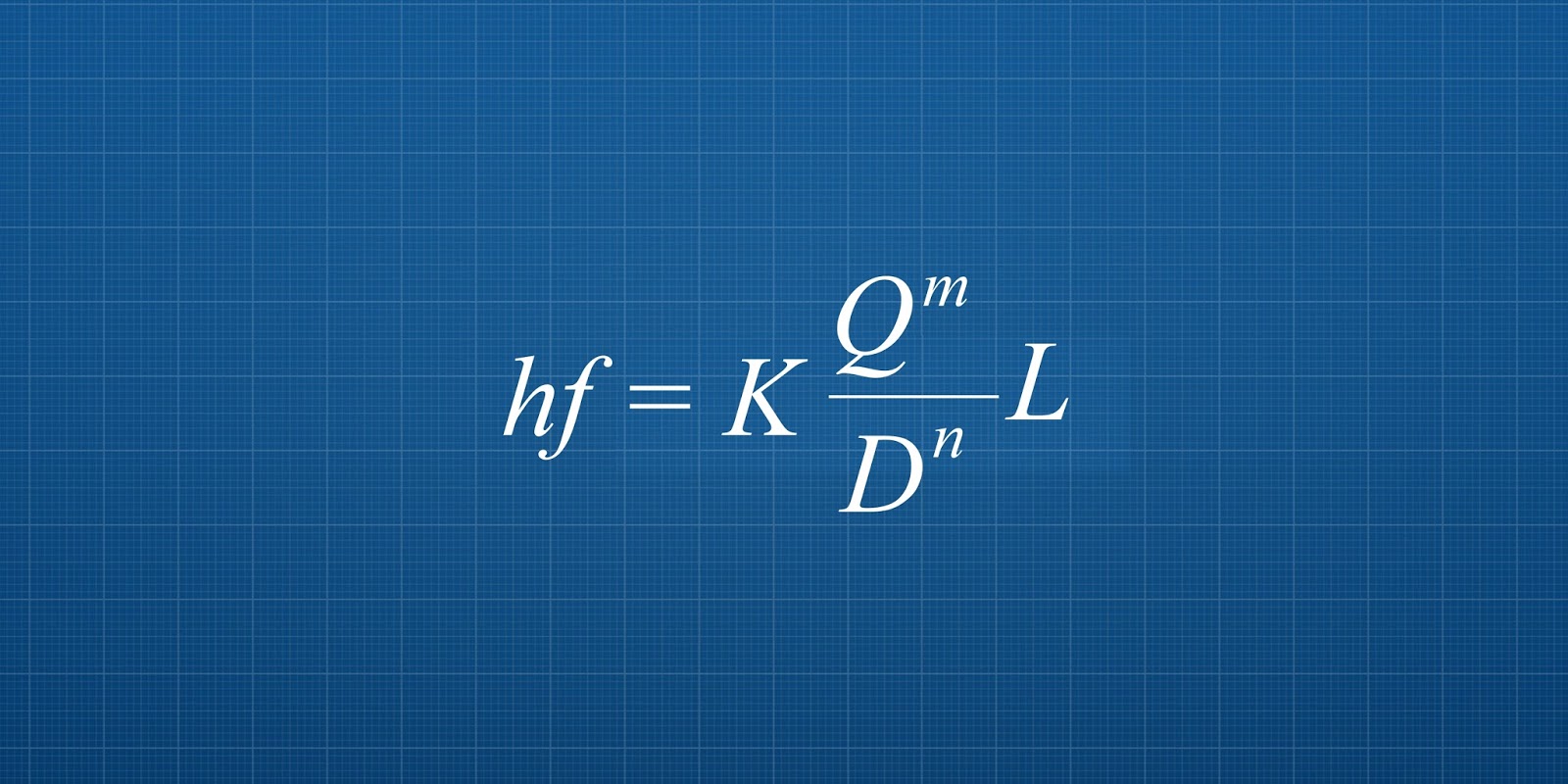




.png)


Comentarios
Publicar un comentario
déjanos tus comentario