Diseño hidráulico de tuberías con salidas múltiples telescópicas (portalaterales y laterales)
Calcular la pérdida de carga permisible (hfp) en la tubería con salidas múltiples, la cual dependiendo de su ubicación en el sistema (lateral o secundaria en aspersión o bien portalateral en sistemas localizados), es igual a un cierto porcentaje P de la carga del emisor he, más la carga de presión que se gana por el desnivel a favor (dn) en la tubería\[hfp=P*he+dn\]
Pseudocodigo
Comentarios Generales: Primero se identifican los dos diametros cuya perdida de carga por fricción son los mas cercanos a la perdida de carga permisible Hfp, posteriormente, mediante métodos numéricos encuentra las longitudes de esos diametros.
Datos de
entrada para sistemas de riego localizado (Pestaña Portalaterales -2D Diámetros de Hf Riego): Superficie de la sección (ha), Lamina Horaria (mm/hr), Separación
entre salidas (laterales) (m), longitud total de la tubería portalateral (m), perdida de carga
permisible (m), este ultimo se puede calcular utilizando la formula descrita en esta entrada del blog o directamente en HFRiego Excel.
Datos de entrada para Aspersión (Pestaña Lateral - 2D Diámetro de HF Riego): Gasto o caudal en cada salida, Separación entre salidas (m), Longitud Total de la tubería (m), pérdida de carga permisible (m)
Comentario:
Sea di, di+1, di+2,…,
dn los diámetros a evaluar, donde i se refiere al diámetro más grande y n el diámetro más pequeño.
Comentario:
F se refiere al factor de salidas múltiples,
hf a la pérdida de carga por fricción
en una tubería ciega, hfs a la pérdida
de carga por fricción en una tubería con salidas múltiples, Hfp perdida de carga permisible, L a la longitud total de la tubería
telescópica.
Inicio de los cálculos:
Se calcula el numero de salidas N // el número de salidas es igual a Longitud total/separación entre salidas y redondear a un valor mas bajo para que sea un número entero
Se calcula el valor del factor de salidas múltiples (F) // se toma en cuenta las salidas en toda la Longitud (L), usar la formula de Scalopi.
Repetir por cada diámetro desde i
hasta n
Calcular la hf en toda la L con la fórmula de Hazen-Williams, Darcy-Weisbach, Manning o Scobey con el diámetro i // se debe emplear los valores de los diametros internos
Calcular hfs: hfs=hf*F // Es la ecuación de perdida de carga por fricción en una tuberia con salidas múltiples Mas información
Comparar (hfs>Hfp) // se compara la perdida de carga por fricción en la tuberías con salidas múltiples (hfs) y la pérdida de carga permisible (Hfp)
Si es falso continuar el
ciclo.
Si es falso y se llega hasta el diámetro n entonces ningún diámetro satisface la pérdida de carga permisible,
enviar mensaje de error y no avanzar a los siguientes pasos.
Sí es verdadero, parar el
ciclo y almacenar el diámetro evaluado en la variable diámetro menor (dm)
y el inmediato anterior evaluado como el diámetro mayor (do), así
como sus respectivas perdidas de carga, donde la pérdida de carga por salidas
múltiples del diámetro menor en L es hfsmt y del diámetro mayor es
hfsot.
Fin de comparación
Comentario: Hasta este punto ya conocemos los dos diametros que satisfacen la condición de la perdida de carga permisible, ahora para encontrar
las dos longitudes (L1 [Longitud del diámetro menor]+L2
[longitud del diámetro mayor]=L) se aplica el método de bisección.
Comentario: C corresponde
al número de salidas, SE separación entre salidas, Q Caudal total, Qs Caudal en
cada salida [constante], dm al diámetro menor y do al
diámetro mayor
Repetir mientras que valor absoluto(Tolerancia)>= 0.0000001
i) A=0
y B=Número total de emisores, por lo que C=(A+B)/2 // Son valores que se usan para le método de bisección
ii) Calcular la Longitud del Diámetro menor-> L1= C*SE // la longitud de la tuberia para el tramo final
iii) Calcular el número de salidas -> NEs=Redondear(C)+1
iv) Calcular la distancia del inicio de la tuberia a la primera salida (S0)->L1 - (NEs - 1) * SE
v) Calcular
el caudal del NEs -> Qs=QSalida(Aspersor o línea lateral)*NEs
Seleccionar una ecuación para estimar perdidas de carga por fricción con el diámetro menor
i) Calcular el valor de F con el número de salidas en L1
ii) Calcular la hfm1 en la longitud L1 con el dm.
iii) Calcular la hfsm1: hfsm1=hfm1*F
Seleccionar una ecuación para estimar perdidas de carga por fricción con el diámetro mayor y la longitud del diámetro menor
i) Calcular el valor de F con el número de salidas
en L1
ii) Calcular la hfo1 en la longitud L1 con el do.
iii) Calcular la hfso1: hfso1=hfo1*F
---Termínanos de calcular pérdidas de carga por fricción con FORMULAS---
Calcular la perdida de carga por fricción en tuberías con salidas múltiples para el diámetro
mayor en la L2: hfsoo= hfsot - hfso1
Calcular la perdida de carga por fricción en la tubería con salidas
múltiples en toda la Longitud considerando los dos diametros: hfst= hfsm1+ hfsoo
Calcular la tolerancia: Tolerancia= hfst- Hfp
Si Tolerancia >= 0.0000001 entonces B = C de lo contrario A = C
Comentario: Si el ciclo se repite una cantidad alta, por ejemplo 1000 veces, significa que puede que no haya convergencia y decirle al usuario que revise sus datos. Se puede cuantificar el numero de veces poniendo un contador dentro del ciclo.
Termina // El ciclo termina si se cumple la tolerancia y se recuperan la longitud L1.
Calcular longitud del diámetro mayor L2 -> L2= L-L1
Devolver el valor de dm,
do, L1 y L2
Fin
de los cálculos.





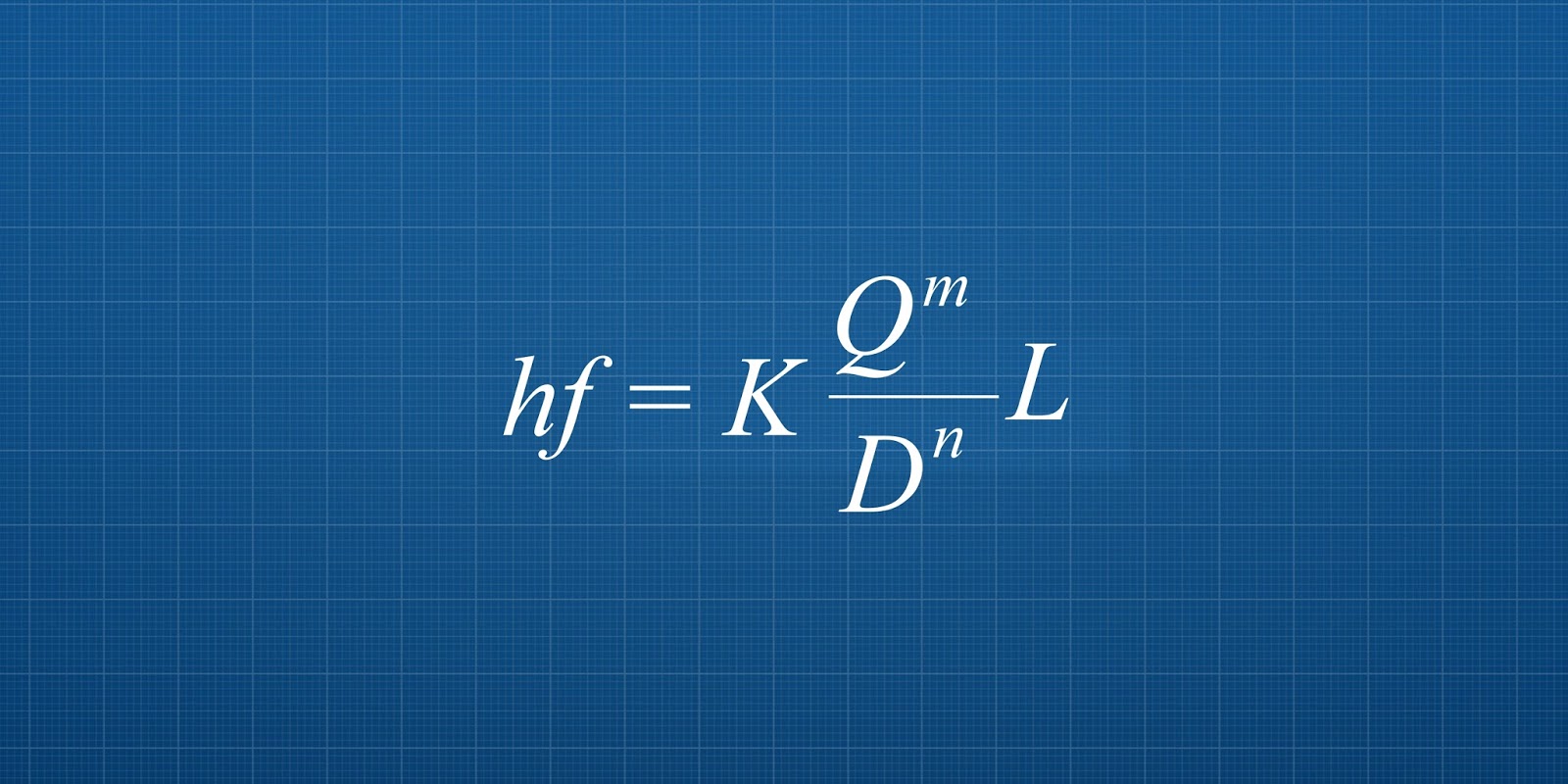


.png)


