Solución de la ecuación de Colebrook-White, con métodos numéricos.
En 1845, Darcy-Weisbach
dedujeron experimentalmente una ecuación para calcular las pérdidas por
cortante (“Fricción”), en un tubo con flujo permanente y diámetro constante
(Ver Ec. 1), en la ecuación propuesta todos los datos eran conocidos excepto
uno al que se le llamó factor de pérdidas (f).
$$hf=f\frac { L }{ D } \frac { { V }^{ 2 } }{ 2g } $$
Dónde: hf: pérdidas por cortante o fricción (m); f: factor de pérdidas por cortante o por fricción (adimensional); g: aceleración de la
gravedad (m2/s); D: diámetro del tubo (m); L: longitud del tubo (m) y V: velocidad media en el
tubo (m/s).
Muchos son los
investigadores que comenzaron a estudiar el fenómeno para poder encontrar una
expresión que permitiera calcular la famosa f, entre ellos se encuentran Colebrook-White:
·
En la región laminar Poiseuille propuso en 1846
la siguiente ecuación:
$$f=\frac { 64 }{ Re } $$
·
En régimen turbulento, normalmente se usa la
ecuación de Colebrook-White.
$$\frac { 1 }{ \sqrt { f } } =-2\log { \left[ \frac { \frac { \varepsilon }{ D } }{ 3.71 } +\frac { 2.51 }{ Re\sqrt { f } } \right] } $$ $$Re=\frac { V\quad D }{ \upsilon }$$
Donde: Re: Número de Reynolds (Adimensional); ε: Rugosidad absoluta (m); ε/D Rugosidad relativa; : viscosidad cinemática del fluido (m²/s);
La ecuación de Colebrook-White se obtiene de las dos
ecuaciones de Nikuradse:
$$\frac { 1 }{ \sqrt { f } } =-2log\quad \left( \frac { \frac { \varepsilon }{ D } }{ 3.71 } \right) $$
y
$$\frac { 1 }{ \sqrt { f } } =-2log\quad \left( \frac { 2.51 }{ Re\sqrt { f } } \right) $$
donde la primera es válida para tubos rugosos con
flujo turbulento totalmente desarrollado y la segunda
es válida para tubos lisos en régimen turbulento. De
tal suerte que al combinarlas se tiene la expresión de Colebrook-White (Guerrero, 1995)
La ecucación de Colebrook-White está basada en estudios experimentales en tuberías comerciales e incluye consideraciones teóricas de los trabajos de von Karman y Prandlt, misma que el propio Lewis F. Moody (1944) afirmó que arrojaban resultados satisfactorios, ya que contempla tuberías lisas y rugosas, de la cual se origina el conocido Diagrama de Moody para obtener de manera gráfica factores de fricción. Lo anterior convierte a la correlación de CW en una ecuación estándar y la más aceptada para la estimación del factor de fricción a régimen turbulento y para rugosidad relativa (0 < ε/D < 0.05) (Anaya-Durand et al., 2014). como se observa en la expresión de Colebrook-White, es imposible resolver analíticamente (despejar el valor de f), por tanto para conocer este valor debemos recurrir a métodos numéricos y hallar de una forma aproximada dicho valor. En este caso se determinará con el método de Bisección.
El método de bisección tiene como característica principal que se debe definir un intervalo en donde posiblemente se encuentre nuestro valor buscado, si el valor buscado no se encuentra dentro de este intervalo la función no convergerá. El intervalo a usar, para este caso, es de [0, 10], el límite inferior igual a cero es porque no tiene caso que nuestra f sea negativa, y el límite superior es 10 debido a que no es posible que se tengan valores de f muy grandes, incluso podemos definir nuestro límite superior igual a 1 para tener el intervalo [0,1]. A continuación se muestra un pseudocodigo para determinar el coeficiente de fricción (f) de la expresión de Colebrook-White usando el método de bisección:
Pseudocodigo
Algoritmo Hf_HW
Definir Re, e, D, A, B, FA, FB, F, C Como Real
Leer Re //Número de Reynolds (Adimensional)
Leer e //Rugosidad Absoluta (m)
Leer D // Diámetro (m)
//Definir intervalo en donde se buscara el valor de f [A,B]
A = 0.0 //Intervalo inferior
B =10 //Intervalo superior
//Inicia ciclo
Repetir
C = (A+B)/2 // calculamos C [Sera el valor del coeficiente f]
FA=1/rc(C) // Evaluamos la ecuación antes del igual con el valor de C.
FB =-2*ln((e/D)/3.71+2.51/(Re*rc(C)))*0.434294481903252 // // Evaluamos la ecuación despues del igual con el valor de C. Se multiplica el logaritmo natural por el número 0.43429 para convertir el logaritmo natural en log10
F = FB-FA
Si
F>
0
Entonces
B=
C
Sino
A=C
FinSi
Hasta Que abs (F) menor o igual a 0.00001
Escribir 'El Factor de Friccion es: ',C
FinAlgoritmo
Matlab code
% Programa que calcula el coeficiente de FricciónDe esta forma podemos hallar el coeficiente de fricción de la expresión de Colebrook-White y usarlo en la ecuación de Darcy-Weisbach.
Si desea calcular el valor de f, debe ingresar los valores solicitados en el siguiente formulario.
Les dejamos esta infografia donde se muestra el proceso de manera resumida. No olvides compartirla
Literatura citada
Anaya-Durand, A. I.,
Cauich-Segovia, G. I., Funabazama-Bárcenas, O., & Gracia-Medrano-Bravo, V.
A. (2014). Evaluación de ecuaciones de factor de fricción explícito para
tuberías. Educacion Quimica.
https://doi.org/10.1016/S0187-893X(14)70535-X
Guerrero Angulo, J. O.
(1995). Ecuación modificada de Colebrook-White. Ingeniería Hidráulica En
Mexico, 10(1), 43–48.
Moody, L. F. (1944). Friction factors for pipe
flow. Transacctions of the American Society of Mechanical Engineers, 66,
671–678.




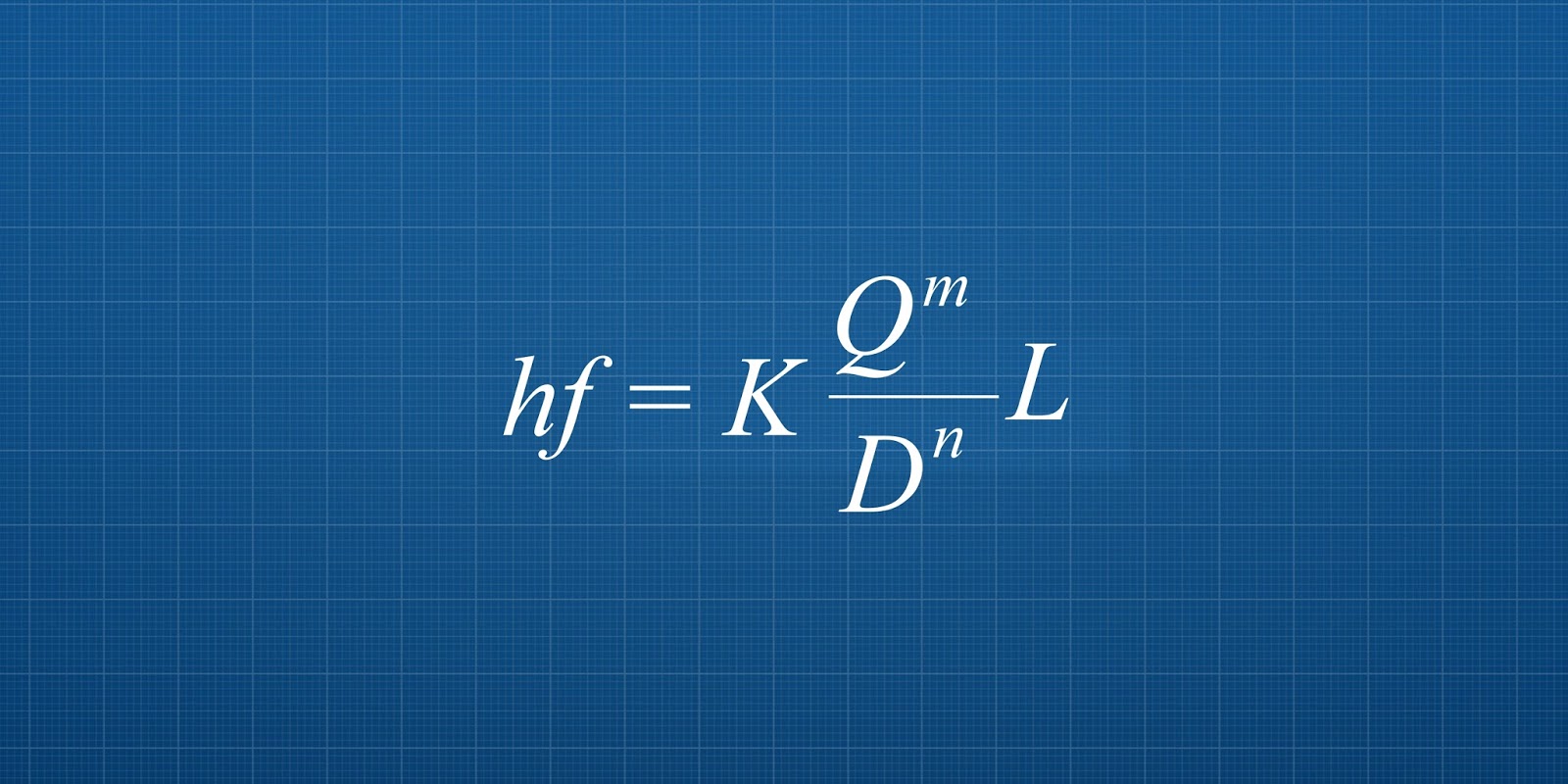

.png)



